Задачи по математическим моделям в экономике. Часть 01
Задача №3114 (составление математической модели и поиск оптимального решения)
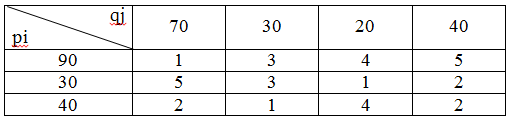
Построить экономико-математическую модель и решить транспортную задачу:
Задание: свести к задаче линейного программирования и воспользоваться средствами Microsoft Office Excel.
Решение задачи:
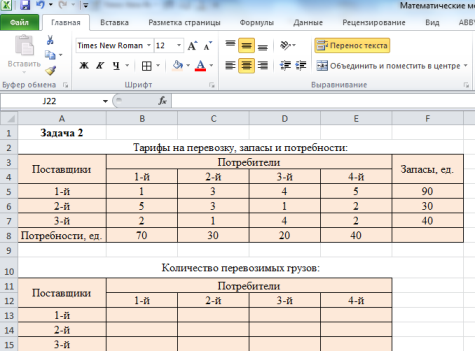
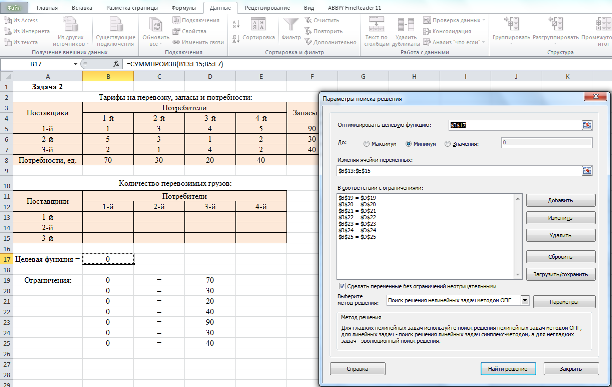
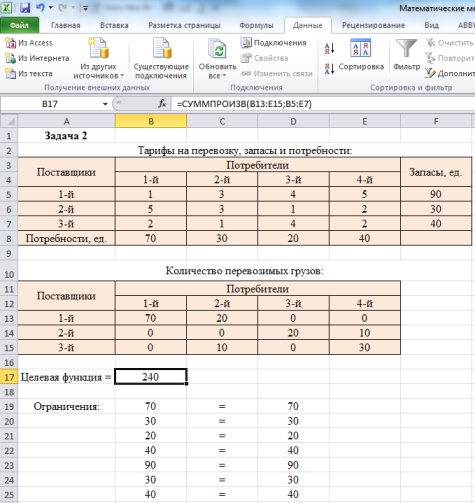
Сводим транспортную задачу к задаче линейного программирования. Обозначаем xi как количество грузов, перевозимых из пункта px в пункт qi. На листе Microsoft Office Excel отражаем исходные данные и массив величин xi:
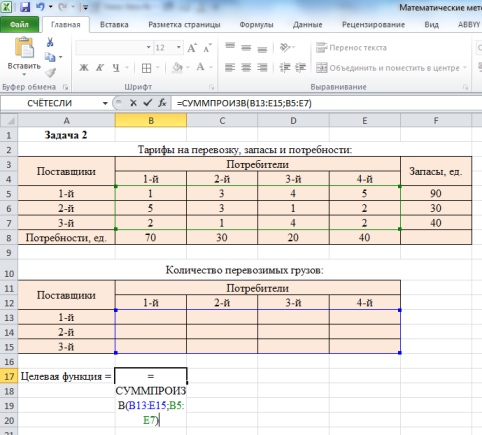
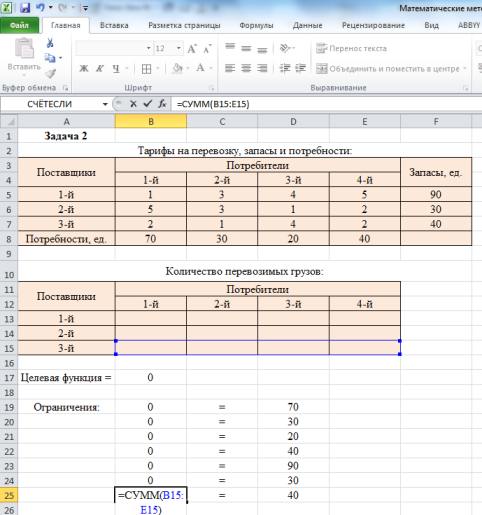
Записываем целевую функцию и ограничения:
Для решения воспользуемся «Поиском решения»:
Ответ: затраты на перевозку грузов будут минимальными (240 ден. ед.), если план перевозки будет следующим:
1-й поставщик отправляет 70 ед. груза 1-му потребителю и 20 ед. груза – 2-му потребителю;
2-й поставщик отправляет 20 ед. груза 3-му потребителю и 10 ед. груза – 4-му потребителю;
3-й поставщик отправляет 10 ед. груза 2-му потребителю и 30 ед. груза – 4-му потребителю.
Все запасы (90+30+40=160 ед.) использованы, все потребности (70+30+20+40=160 ед.) удовлетворены.
Обновить
Предложение поставщиков (ед.):
Спрос потребителей (ед.):
Матрица затрат на доставку единицы груза от каждого поставщика потребителю (руб.):
1. Составить математическую модель оптимизации перевозок.
2. Определить исходный опорный план перевозок.
3. Найти оптимальный план перевозок методом потенциалов и соответствующие ему минимальные транспортные затраты.
Перейти к демонстрационной версии решения задачи
Задача фирмы заключается в том, чтобы найти план выпуска, обеспечивающий получение максимальной выручки от реализации готовой продукции.
Требуется:
1. Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программирования.
2. Используя графический метод решения, найти оптимальный план выпуска продукции.
3. Составив двойственную задачу, к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения.
Перейти к демонстрационной версии решения задачи
Требуется оценить характеристики работы фирмы по ремонту радиоаппаратуры.
Перейти к демонстрационной версии решения задачи
Для расширения производства совет директоров выделяет средства в объеме 250 млн. руб. с дискретностью 50 млн. руб. Прирост выпуска продукции на предприятиях зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблицах по вариантам.
Найти распределение средств между предприятиями, обеспечивающее максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить не более одной инвестиции.
Исходные данные:
Перейти к демонстрационной версии решения задачи
Сформулировать задачу ЛП.
Перейти к демонстрационной версии решения задачи
при ограничениях:
Перейти к демонстрационной версии решения задачи
Караван Марко Поло использует для перевозки сухого инжира из Багдада в Мекку дромадеров (одногорбых верблюдов) и обычных (двугорбых) верблюдов. Верблюд может нести 1000 фунтов груза, а дромадер – 500 фунтов. За время пути верблюд потребляет 3 тюка сена и 100 галлонов воды, а дромадер – 4 тюка сена и 80 галлонов воды. Вдоль пути Марко Поло имеются пункты снабжения, расположенные в оазисах. Общая емкость запасов на этих участках 1600 галлонов воды и 60 тюков сена. Верблюды и дромадеры нанимаются у пастуха около Багдада. Стоимость аренды верблюда составляет 11 монет, а дромадера – 5 монет. Караван должен доставить из Багдада в Мекку не менее 10000 фунтов инжира.
Перейти к демонстрационной версии решения задачи
1) Возможно ли с помощью алгоритма итераций «нащупать» равновесную цену? Если да, то перейти к п. 2.
2) Провести несколько итераций нахождения равновесной цены с указанием дефицита и профицита товаров.
3) С каждой единицы товара повседневного спроса взимается налог t. Выяснить, какую часть налога t оплачивает покупатель, а какую часть производитель? Найти суммарную стоимость продаж до и после введения налога.
Исходные данные взять самостоятельно по согласованию с руководителем.
Перейти к демонстрационной версии решения задачи
Перейти к демонстрационной версии решения задачи
а) Начертить графики дохода, прибыли, издержек. По критерию максимальной прибыли найти оптимальные: объем производства, цену, значения прибыли и издержек.
б) Решить ту же задачу с учетом налогообложения – с каждой единицы произведенной и реализованной продукции взимается налог в размере t руб. Найти зависимости y(t), p(t). Построить кривую Лаффера и график прибыли, зависящий от величины налоговой ставки t. Найти точку, где G(t) максимальна, и точку замирания деловой активности.
Перейти к демонстрационной версии решения задачи
а всего работников
Основные фонды оцениваются в
Найти параметры производственной функции.
Перейти к демонстрационной версии решения задачи
Перейти к демонстрационной версии решения задачи
построить карту кривых безразличия, найти предельную норму замены благ и в общем виде оптимальную функцию спроса. Найти оптимальную точку спроса при ценах (р1=8, р2=2) и доходе М=64. Дать графическую интерпретацию решения.
Перейти к демонстрационной версии решения задачи
Перейти к демонстрационной версии решения задачи
Исходные данные:
матрица затрат продукции:
матрица выпуска продукции:
вектор запаса продуктов на начало моделирования:
вектор цен на продукцию:
Найти интенсивности применения производственных способов, которые позволяют в конце первого периода получить продукцию максимально возможной стоимости.
Перейти к демонстрационной версии решения задачи
Исходные данные:
матрица прямых затрат продукции:
вектор конечного выпуска:
1. Проверите модель на продуктивности:
а) с помощью теоремы Фробениуса-Перрона;
б) с помощью признаков продуктивности.
2. Если модель продуктивна, найти валовые выпуски отраслей, межотраслевые потоки, составить таблицу межотраслевого баланса.
Перейти к демонстрационной версии решения задачи
Исходные данные:
фактор шкалы = 3;
доля материальных затрат в совокупном продукте = 0,3;
коэффициент эластичности выпуска по затратам фондов = 0,7;
доля инвестирования в конечном продукте = 0,8;
доля износа фондов = 0,12;
темп прироста трудовых ресурсов = 0,03.
В предположении, что технология описывается производственной функцией Кобба-Дугласа, найдите фондовооруженность труда, производительность труда и удельное непроизводственное потребление в стационарном режиме. Раскройте понятие и найдите значение оптимальной доли инвестирования и те же показатели с учетом «золотого правила» накопления».
Перейти к демонстрационной версии решения задачи
Перейти к демонстрационной версии решения задачи