Задачи по эконометрике. Часть 01
Задача №62 (определение зависимости между спросом и ценой для установления цены на услугу)
Предприятия предоставляет услуги населению. Поскольку действующие цены не покрывают расходов, связанных с предоставлением услуг населению, возникла задача повышения цен.
Результаты заказанного с этой целью исследования дали возможность составить прогноз спроса на услугу в зависимости от цены:
| Цена услуги, ден. ед. | Количество клиентов в год, млн. чел. |
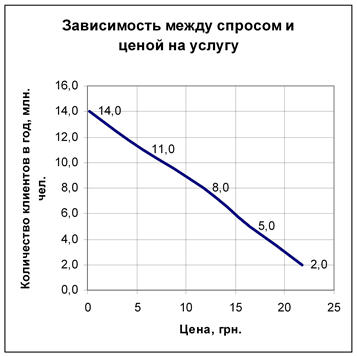
| 21,8 | 2 |
| 16,4 | 5 |
| 11,8 | 8 |
| 5,6 | 11 |
| 0,2 | 14 |
Определить зависимость между спросом и ценой для установления цены на услугу.
Решение задачи:
Построим график изменения объема продаж в зависимости от колебаний цены на услугу:
Функцию зависимости спроса от цены определяем, используя метод наименьших квадратов. Для этого строим вспомогательную таблицу и решаем соответствующие системы уравнений:
сумм(y)=na0+a1*сумм(x); сумм(yx)=a0*сумм(x)+a1*сумм(x)2; где x - цена, ден. ед., e - спрос на услугу, млн. чел.
Вспомогательная таблица для определения функций спроса и предложения
| № | Цена, ден. ед. – Xi | Xi2 | Спрос, млн. чел. –Yi | XiYi |
| 1 | 21,8 | 475,2 | 2 | 43,6 |
| 2 | 16,4 | 269,0 | 5 | 82,0 |
| 3 | 11,8 | 139,2 | 8 | 94,4 |
| 4 | 5,6 | 31,4 | 11 | 61,6 |
| 5 | 0,2 | 0,0 | 14 | 2,8 |
| Итого | 55,8 | 914,8 | 40,0 | 284,4 |
Система уравнений имеет вид:
5а0+55,8а1=40,0;
55,8а0+914,8а1=284,4.
Решение системы: а0=14,189; а1=-0,555.
Функция спроса имеет вид:
у=14,189-0,555х.
Обновить
Требуется:
1. Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
2. Сделать прогноз на 2 уровня вперед.
Вариант 1
t – годы; yt – собственная продукция.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Требуется (для всех вариантов):
1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
3. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации.
4. С помощью частных F-критериев Фишера и t-статистики Стьюдента оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1.
5. По возможности составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Обозначения и наименование показателей производственно-хозяйстве нной деятельности предприятий:
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
1. Для характеристики y от x построить следующие модели:
линейную,
экспоненциальную,
гиперболическую.
2. Оценить каждую модель, определив:
индекс корреляции,
коэффициент детерминации,
F-критерий Фишера.
3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
4. По лучшей модели рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 10% относительно его среднего уровня.
5. На графике отобразить диаграмму рассеяния, график лучшей модельной кривой и прогнозное значение.
Вариант 1
х – имущество (в тыс. $) семи случайно выбранных семей,
у – накопления (в тыс. $).
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Таблица 1 – Исходные данные
1. Постройте прогноз численности наличного населения города Г на 2012-2013 гг., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните результаты, сделайте вывод.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Таблица 1 – Результаты работы магазинов
Перейти к демонстрационной версии решения задачи
2. Рассчитайте параметры уравнений, объясните их смысл:
2.1. Линейной парной регрессии y=a+b*x.
2.3. Полулогарифмической парной регрессии y=a+b*lnx.
2.5. Степенной парной регрессии Y=a*x^b.
3. Оцените качество каждой модели, для этого:
3.1. Рассчитайте коэффициент детерминации R^2.
3.2. Проверьте статистическую значимость результатов регрессионного моделирования с помощью F-критерия Фишера (уровень значимости 0,05).
3.3. Рассчитайте среднюю ошибку аппроксимации.
3.4. Рассчитайте средний коэффициент эластичности.
3.5. Сделайте выводы.
4. По значениям характеристик каждого уравнения выберите лучшее уравнение и дайте обоснование.
5. С помощью лучшего уравнения регрессии выполните прогноз, если прогнозное значение фактора увеличится на 10% от своего среднего уровня.
6. Для линейного уравнения парной регрессии определите доверительный интервал прогноза для уровня значимости 0,05.
Исходные данные:
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Требуется:
1. Проверить гипотезу о наличии тренда во временном ряде.
2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.
3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,9.
4. Дать точечный и интервальный прогноз выпуска продукции на 2010 г. с надежностью 0,9.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Требуется:
1. Построить корреляционное поле между накоплениями и доходом. Выдвинуть гипотезу о тесноте и виде зависимости между накоплениями и доходом.
2. Оценить тесноту линейной связи между накоплениями и доходом с надежностью 0,95.
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости накоплений от дохода.
4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,95 и построить для них доверительные интервалы.
5. Рассчитать коэффициент детерминации. С помощью F-критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,95.
6. Для домохозяйства с доходом 43,8 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,95.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии для зависимости накоплений от дохода и стоимости имущества. Пояснить экономический смысл его параметров.
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,95 и построить для них доверительные интервалы.
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
11. С помощью F-критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,95.
12. Для домохозяйства с доходом 43,8 ден. ед. и стоимостью имущества 52,1 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,95.
13. Проверить построенное уравнение на наличие мультиколлинеарности по критерию Стьюдента; критерию χ2. Сравнить полученные результаты.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Требуется:
1. Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
2. Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
3. Сделать прогноз на 2 квартала вперед.
Исходные данные:
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Таблица 2.1 – Исходные данные
Требуется:
1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации.
5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора X1 после X2 и фактора X2 после X1.
6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Требуется:
1. Построить линейное уравнение парной регрессии y от x.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике построить исходные данные и теоретическую прямую.
Данные о зависимости среднедневной заработной платы от среднедушевого прожиточного минимума в день на одного трудоспособного:
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Имеются следующие данные по 20 предприятиям:
Перейти к демонстрационной версии решения задачи
1. Постройте линейное уравнение регрессии с одной объясняющей переменной.
2. Дайте экономическую интерпретацию коэффициента регрессии.
3. Выполните корреляционный анализ, т.е. вычислите линейный коэффициент корреляции и теоретическое корреляционное отношение (индекс корреляции). Сделайте вывод о тесноте и направленности связи между Y и X.
4. Вычислите коэффициент детерминации. Сделайте вывод.
5. Выполните дисперсионный анализ. Протестируйте статистическую гипотезу о достоверности уравнения регрессии при уровне значимости α=0,05. Сделайте вывод.
6. Вычислите среднюю относительную ошибку аппроксимации. Сделайте вывод о возможности использования регрессионной модели для прогнозирования и управления.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Исходные данные:
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Рассчитать коэффициент корреляции. Данные расчетов оформить в виде таблицы.
Перейти к демонстрационной версии решения задачи
Сформулируйте выводы и дайте рекомендации.
Перейти к демонстрационной версии решения задачи
В качестве примера прямолинейной зависимости между факторным и результативным показателем используйте данные об изменении уровня выработки рабочих (Y) в зависимости от уровня фондовооружённости труда (X), представленные в таблице.
Исходные данные:
Перейти к демонстрационной версии решения задачи
Перейти к демонстрационной версии решения задачи
В качестве примера прямолинейной зависимости между факторным и результативным показателем используйте данные об изменении уровня выработки рабочих (Y) в зависимости от уровня фондовооружённости труда (X), представленные в таблице:
Перейти к демонстрационной версии решения задачи
Охарактеризуйте связь между данными признаками через коэффициент Спирмена.
Перейти к демонстрационной версии решения задачи
Таблица 1 – Исходные данные
Перейти к демонстрационной версии решения задачи
Модель денежного и товарного рынков:
где R – процентные ставки,
Y – реальный ВВП,
M – денежная масса,
I – внутренние инвестиции,
G – реальные государственные расходы.
Задание:
1. Для каждого уравнения модели определите его идентифицируемость, применив необходимое и достаточное условие идентификации.
2. Определите метод оценки параметров модели.
3. Запишите в общем виде приведенную форму модели.
Перейти к демонстрационной версии решения задачи
Задание:
1. Построить автокорреляционную функцию.
2. Сделать вывод о наличии сезонных колебаний.
3. Построить аддитивную модель временного ряда (для нечетных вариантов).
4. Сделать прогноз на 2 квартала вперед.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Задание:
1. Постройте линейную модель множественной регрессии.
2. Запишите стандартизированное уравнение множественной регрессии. На основе стандартизированных коэффициентов регрессии и средних коэффициентов эластичности ранжируйте факторы по степени их влияния на результат.
3. Найдите коэффициенты парной, частной и множественной корреляции. Проанализируйте их.
4. Найдите скорректированный коэффициент множественной детерминации. Сравните его с нескорректированным (общим) коэффициентом детерминации.
5. С помощью F-критерия Фишера оцените статистическую надежность уравнения регрессии и коэффициента детерминации.
6. С помощью частных F-критериев Фишера оцените целесообразность включения в уравнение множественной регрессии фактора Х1 после Х2 и фактора Х2 после Х1.
7. Составьте уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи
Расчеты производить в Excel «Анализ данных», меню – Сервис.
Отчет оформлять в Word, для ввода формул использовать Equation.
Исследования построенной модели произвести по порядку в соответствии с перечисленными в бланке выполнения задания пунктами.
Исходные данные. В течение года i-я семья, имеющая располагаемый доход xi затратила на приобретение этого товара Vi, руб.
Задание:
1. Подберите модель зависимости, в которой эластичность потребления рассматриваемого товара по отношению к располагаемому доходу не зависит от размера располагаемого дохода.
Замечание. Постоянство эластичности предполагает оценивание модели, линейной в логарифмических уровнях.
2. Постройте график подбора значений регрессии.
3. Рассчитайте среднюю ошибку аппроксимации. Сделайте выводы.
4. Проверьте значимость подобранной модели на уровне α=0,05.
Замечание. Используйте коэффициент детерминации и критерий Фишера.
5. Оцените значение объясняемой переменной при Х=153000.
6. Найдите 95%-ные доверительные интервалы для среднего и индивидуального значения объясняемой переменной при том же значении Х.
7. Найдите с надежностью 0,95 интервальные оценки параметров уравнения регрессии α и β, дисперсии ошибок var(ɛ). Сделайте выводы.
8. Оцените значение объясняемой переменной при Х=153000.
9. С помощью графического метода оцените соответствие используемых для построения модели статистических данных стандартным предложениям регрессионного анализа.
10. В рамках подобранной модели проверьте гипотезы о том, что потребление данного товара эластично по отношению к располагаемому доходу.
Замечание. Эластичное потребление соответствует значению эластичности, большему единицы по абсолютной величине.
11. В рамках подобранной модели проверьте гипотезы о том, что потребление данного товара неэластично по отношению к располагаемому доходу.
Решение данной задачи включает файл в формате Excel.
Перейти к демонстрационной версии решения задачи