Задачи по финансовой математике. Часть 10

Задача №480 (расчет срока консолидированного платежа)

Три платежа 8000 руб. со сроком 125 дней, 10000 руб. со сроком 175 дней и 4000 руб. со сроком 200 дней заменяются одним в размере 21000 руб. Стороны договорились об использовании простой процентной ставки 28% годовых. Определить срок консолидированного платежа при базе Тгод=365.

Решение задачи:

Для определения величины консолидированного платежа определяем наращенную стоимость каждого из платежей. Для этого используем формулу простых процентов:

Формула простых процентов

Поскольку в данном случае условие оперирует сроками, выраженными в днях (d), формула приобретает следующий вид:

Формула для расчета срока консолидированного платежа

Записываем выражения для определения наращенной суммы по каждому платежу:

Расчет элементов срока консолидированного платежа

Сумма этих платежей должна составить величину консолидированного платежа:

Расчет срока консолидированного платежа

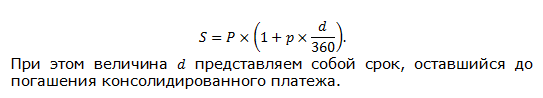
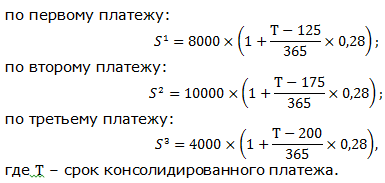
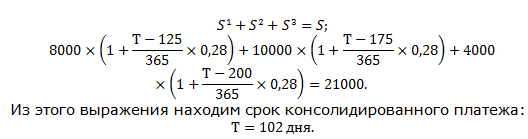
Обновить  

 
# Задача №8289 (расчет продолжительности ссуды) — Администратор 16.07.2020 19:08
Какова была продолжительность ссуды, если долг в 50000 руб. вырос до 80000 руб. при годовой ставке простых процентов i = 30%?
 
 
# Решение задачи №8289 — Администратор 16.07.2020 19:08
Наращенная стоимость по схеме простых процентов рассчитывается по формуле:
FV=PV*(1+i*n),
где PV – первоначальная стоимость, руб.,
i – годовая процентная ставка, доли единицы,
n – продолжительность ссуды, лет.
Из приведенной формулы выражаем продолжительность ссуды:
1+i*n=FV/PV,
i*n=FV/PV-1,
n=(FV/PV-1)/i=(80000/50000-1)/0,3=2 года.
Таким образом, продолжительность ссуды составляет 2 года.
 
 
# Задача №7181 (расчет срока консолидированного платежа) — Администратор 06.07.2020 13:46
Принято решение объединить три платежа стоимостью 10 000 долл., 20 000 долл. и 15 000 долл., срок уплаты которых наступит соответственно через 135, 166 и 227 дней от настоящего момента времени, в один платеж, равный им по сумме. Определить срок консолидированного платежа при использовании простой процентной ставки 8% годовых.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №5831 (расчет срока ренты) — Администратор 14.07.2018 16:05
Определите срок ежегодной ренты в 200 дол., для того, чтобы накопить 2500 дол., если рента копится под 13% годовых.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №5830 (расчет срока отсрочки платежа) — Администратор 14.07.2018 16:05
Заемщик должен вернуть 200 тыс. дол. через 28 дней и 500 тыс. дол. через 75 дней. Он просит консолидировать платежи и согласен вернуть 700 тыс. дол. На какую отсрочку может рассчитывать заемщик при одной и той же 12%-ной годовой ставке?
Перейти к демонстрационной версии решения задачи
 
 
# Задача №5824 (расчет срока возврата кредита) — Администратор 14.07.2018 15:53
По условиям кредита его можно вернуть в любой удобный для заемщика момент в течение года. Кредит дан под 52% годовых с помесячной уплатой процентов. Взяв кредит в сумме 1 млн. руб. в начале года, предприниматель вкладывает средства в торговые операции каждый раз сроком на один месяц, получая 20% прибыли на вложенный капитал. Как наилучшим образом предприниматель может спланировать свои взаимоотношения с банком, если на иные кредиты ему рассчитывать не приходится и через год он сворачивает дело?
Перейти к демонстрационной версии решения задачи
 
 
# Задача №5823 (расчет срока отсрочки платежа) — Администратор 14.07.2018 15:53
Заемщик должен вернуть 100 тыс. дол. через 62 дня и 600 тыс. дол. через 105 дней. Он просит консолидировать платежи и согласен вернуть 700 тыс. дол. На какую отсрочку может рассчитывать заемщик при одной и той же 12%-ной годовой ставке?
Перейти к демонстрационной версии решения задачи
 
 
# Задача №3265 (расчет суммы консолидированного платежа) — Администратор 02.01.2017 13:02
Для ремонта сельхозтехники фермер взял три кредита: 0,4 млн. руб., 0,7 млн. руб., 1,0 млн. руб. со сроками уплаты соответственно через 80, 100 и 150 дней, которые по финансовым обстоятельствам заменяются одним кредитом со сроком уплаты через 210 дней при простой ставке 10%. Найти сумму консолидированного платежа (год принять равным 360 дней).
Перейти к демонстрационной версии решения задачи
 
 
# Задача №2938 (расчет консолидированного платежа) — Администратор 11.12.2016 12:12
Три платежа 3500 руб. со сроком 3 года, 8000 руб. со сроком 4 года и 5000 руб. со сроком 5 лет заменяются двумя, причем через 1,5 года выплачивается 2000 руб., а остаток – через 5,5 лет. Стороны договорились об использовании сложной процентной ставки 30% годовых. Определить остаток долга.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №2812 (расчет суммы консолидированного платежа) — Администратор 05.12.2016 09:41
Решено консолидировать два платежа со сроками 20.04 и 10.05 и суммами платежа 20 тыс. руб. и 30 тыс. руб. Срок консолидации платежей 31.05. Определить сумму консолидированного платежа при условии, что ставка равна 10% годовых.
Перейти к демонстрационной версии решения задачи
 
 
# Задача №2489 (расчет стоимости объединенного векселя) — Администратор 17.11.2016 21:01
Фирма просит векселедержателя переписать три векселя номинальной стоимостью 30, 40, 50 руб. со сроками погашения 60, 80, 70 дней в один вексель со сроком погашения 100 дней. Объединение должно происходить по ставке простых процентов, равной 20%. Определить стоимость объединенного векселя (проценты простые).
Перейти к демонстрационной версии решения задачи
 
 
# Задача №2438 (расчет срока консолидированного платежа) — Администратор 16.11.2016 11:06
Принято решение объединить три платежа стоимостью 10000 долл., 20000 долл. и 15000 долл., срок уплаты которых наступит соответственно через 135, 166 и 227 дней от настоящего момента времени, в один платеж стоимостью 500000 руб. Определить срок консолидированного платежа при использовании простой процентной ставки 6% годовых.
 
 
# Решение задачи №2438 — Администратор 26.07.2017 15:15
 

Информация для заказа задач, которые отсутствуют в нашей базе готовых решений,
всегда в закрепленном материале на странице нашего сообщества Задачи по экономическим дисциплинам.